Указатели
Дедекинд Рихард Юлиус Вильгельм(06.10.1831 — 12.02.1916)
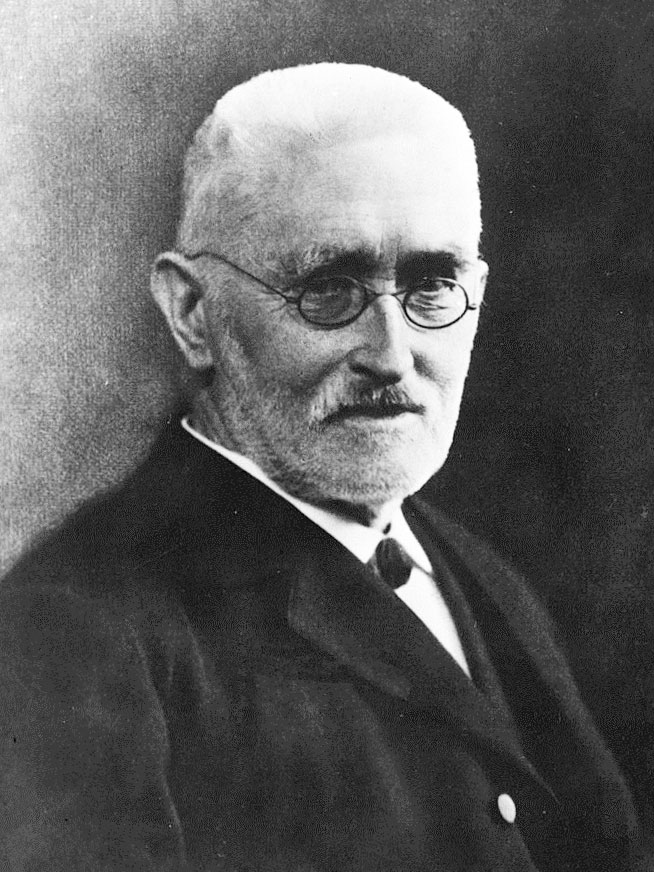
Немецкий математик. Член Берлинской Академии наук (1880), Парижской Академии наук (1910). Окончил Гёттингенский университет. Ученик К. Гаусса и П. Г. Дирихле. Преподавал в университете Гёттингена, Техническом университете Цюриха (с 1858). Был профессором Высшей технической школы в Брауншвейге (1862—1912). Основные труды в области математического анализа, общей алгебры, теории чисел и оснований математики. Обобщив теорию многочленов и алгебраических чисел, ввел в математику понятия решетки, кольца и идеала. Одним из первых дал строгое теоретико-множественное обоснование теории действительных чисел. Сформулировал определение отображения.
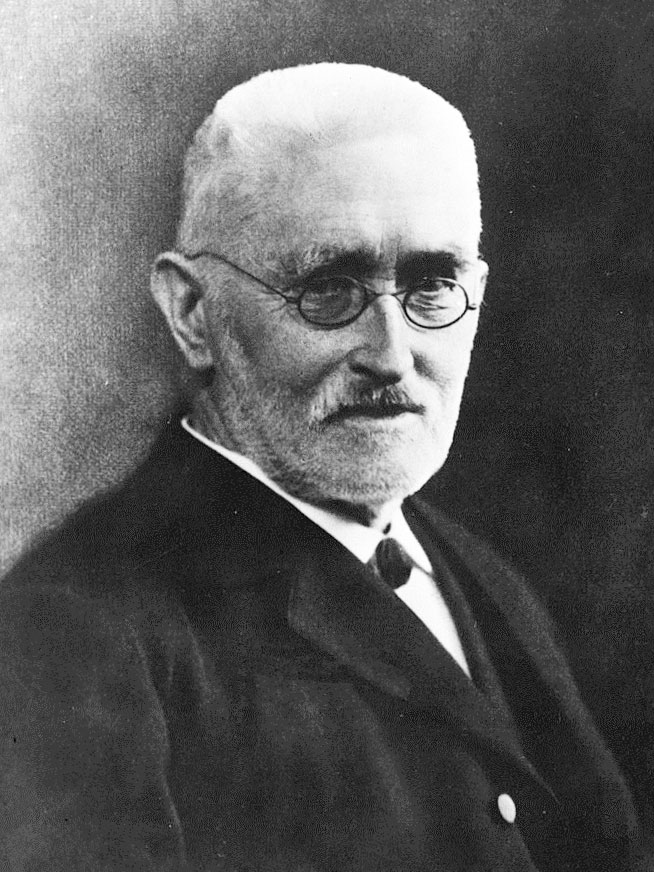
Дедекинд Рихард Юлиус Вильгельм
(06.10.1831 — 12.02.1916)
Авторские труды
 Дедекинд Р. Что такое числа и для чего они служат? / пер. с нем. Н. Парфентьева ; под общ. ред. Г. И. Синкевич. — [2-е изд.]. — М. ; Ижевск : НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2015. — 98 с.
Дедекинд Р. Что такое числа и для чего они служат? / пер. с нем. Н. Парфентьева ; под общ. ред. Г. И. Синкевич. — [2-е изд.]. — М. ; Ижевск : НИЦ «Регулярная и хаотическая динамика», Институт компьютерных исследований, 2015. — 98 с.